on hackathons, pointclouds, and simplicity
over the course of this years autumn holiday, i had the opportunity to participate in my first hackathon; an ai and ml innotech event, hosted by nne (novo nordisk engineering) in partnership with clearedge3d.
i was particularly excited as this was a good opportunity to actually write code that can solve a real world problem; a good chance to get out of "tutorial hell". i sent my application, it was accepted, and i was good to go.
the first day started off with the problem being introduced to us. i did sign an agreement, so i can say that the problems involved point clouds from 3d scans, and that the first task was classify these point clouds and be able to infer what kind of object these point clouds represent.

above is an example of a point cloud that represents a spinning donut.
a point cloud is essentially a collection of dots floating in 3d space, like a virtual constellation. each dot, or "point," represents a specific spot on the surface of a real-world object, captured by a scanner or other sensor. imagine taking a 3d snapshot of, say, a coffee mug; each point in the cloud marks a part of its surface.
what's neat is that when you put all these points together, they start forming the shape of the object. however, unlike a full 3d model, a point cloud doesn't "connect the dots" to make solid surfaces; it leaves them as they are. this makes point clouds both lightweight and detailed, perfect for applications like virtual reality, autonomous cars (to "see" their surroundings), and, in my case, training models to recognize objects.
i'm pretty sure i am not allowed to show any of their data, so you'll just have to take me on my word that their scanning data looked really cool; the different classes were column beams, hvac ducts, i-beams, and pipes, generally things you could find in an industrial facility. these objects were enclosed in a bounding box, this basically means a box that designates the volume that the object is in.

i was introduced to my team, a group of masters students, mostly from dtu, and we started getting to work. in our case, this meant 3 hours of installing libraries and getting the demos they provided us to work on our machines. 2 of our group members dropped out after the first day; and then there were two; me, and a masters student at dtu, left in our group.
the first couple of days of the hackathon i was busy doing the unglamorous work; data preprocessing and cleaning. i had to use the python class that the hosts of the event created to grab exactly the kind of data we needed. once this was done, i started doing a couple of experiments; a linear discriminant analysis on the dimensions of the bounding box for each object. i was basically trying to see if we could extract any information about these objects based purely off their size.
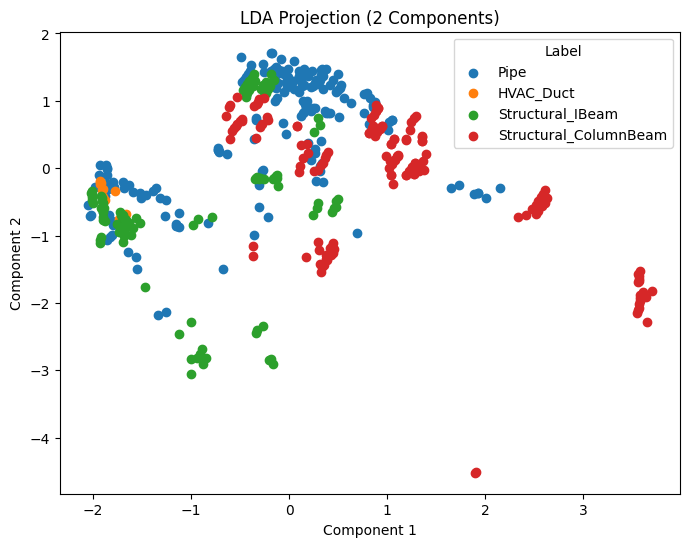
the separation we saw was decent with a linear discriminant analysis, so i figured maybe we could try a quadratic discriminant analysis, to see if we could extract some more complex relationships out of the size of these objects.
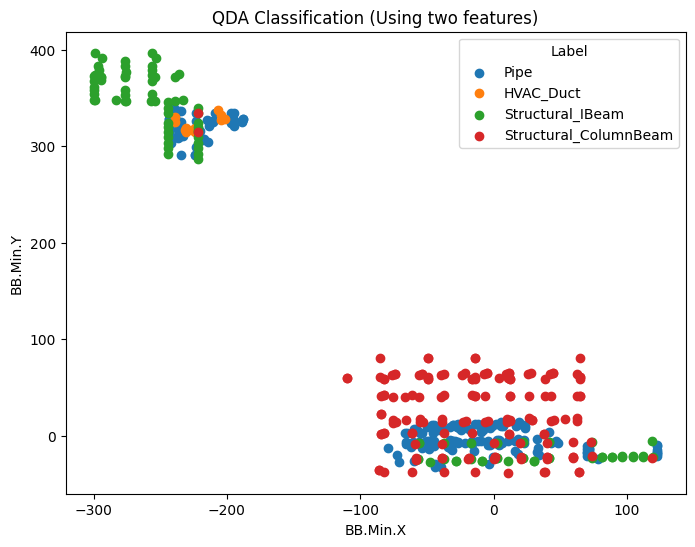
clearly the separation was good here, and while my group mate was putting together a 3d convolutional network (more on this later), i decided to throw together a simple multilayer perceptron to see if we could maybe shortcut our way to the winners podium, by avoiding having to look at the point clouds themselves, and just look at how big the boxes were that contained these point clouds (foreshadowing!!).
strangely enough, i could not for the life of me get this code to run, and we decided to focus on what we deemed to be the more desirable solution; a 3d convolutional network.
3d convolutional networks (3d cnns) are neural networks that specialize in analyzing data with three spatial dimensions, like point clouds or 3d medical scans. unlike regular 2d cnns, which are great for flat images, 3d cnns go a step further to capture depth information. each "convolution" (a fundamental process where filters scan through data) sweeps over height, width, and depth, allowing the network to understand the full 3d structure of an object, like layers of texture and spatial arrangement.
here's an animation (courtesy of geeksforgeeks), showing how a 2d convolution can scan a kernel over a 2d image. the kernel slides (or "convolves") across the image, stopping at every possible 3x3 section. each time it stops, the kernel multiplies its values with the values of the image pixels it's covering, then sums these products to produce a single new value. this new value tells us something about that part of the image, like how "edgy" or "textured" it is.
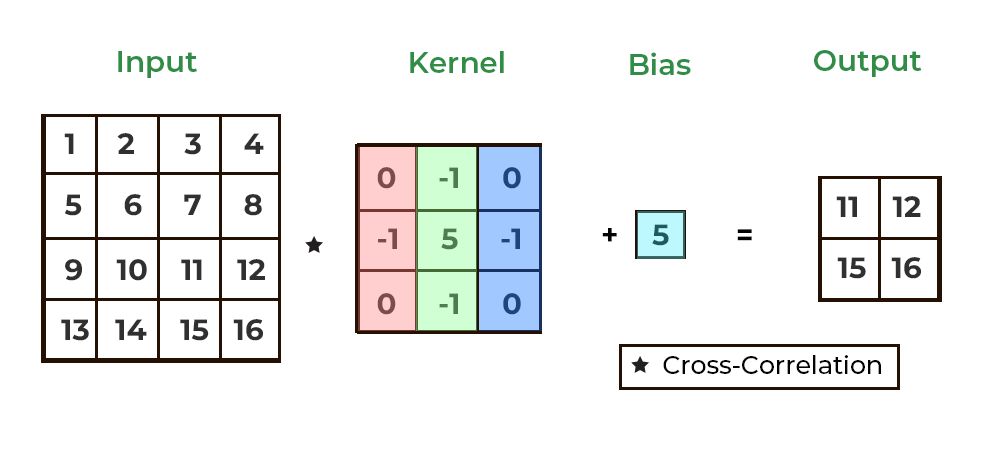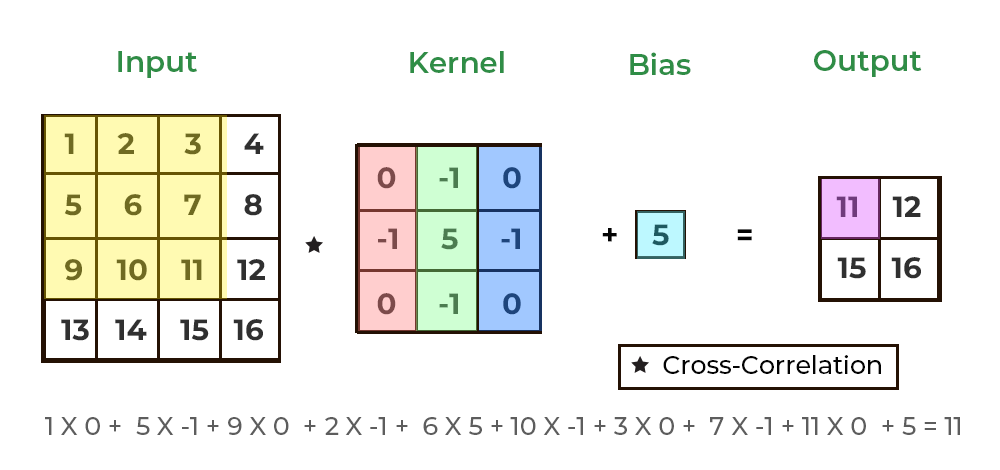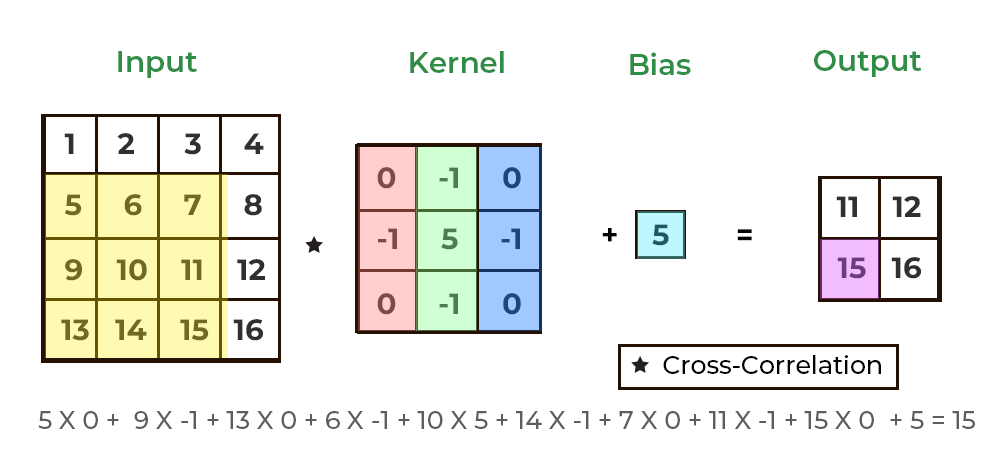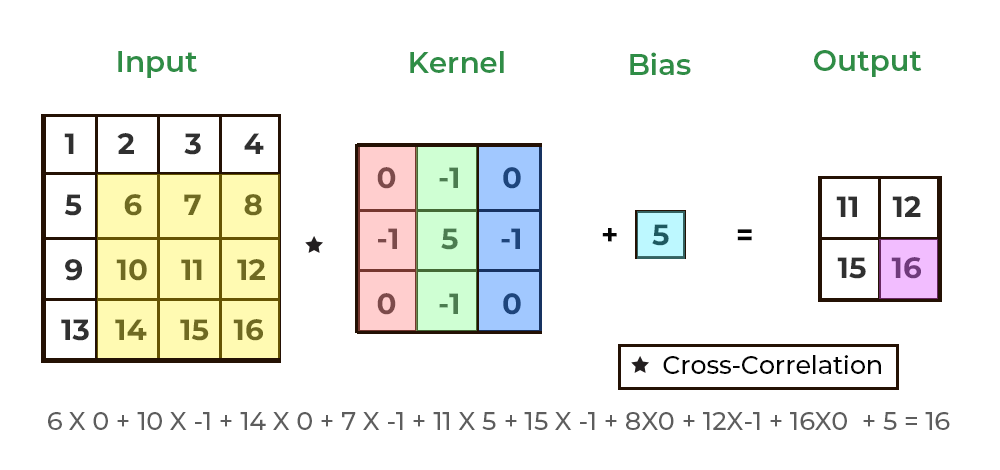
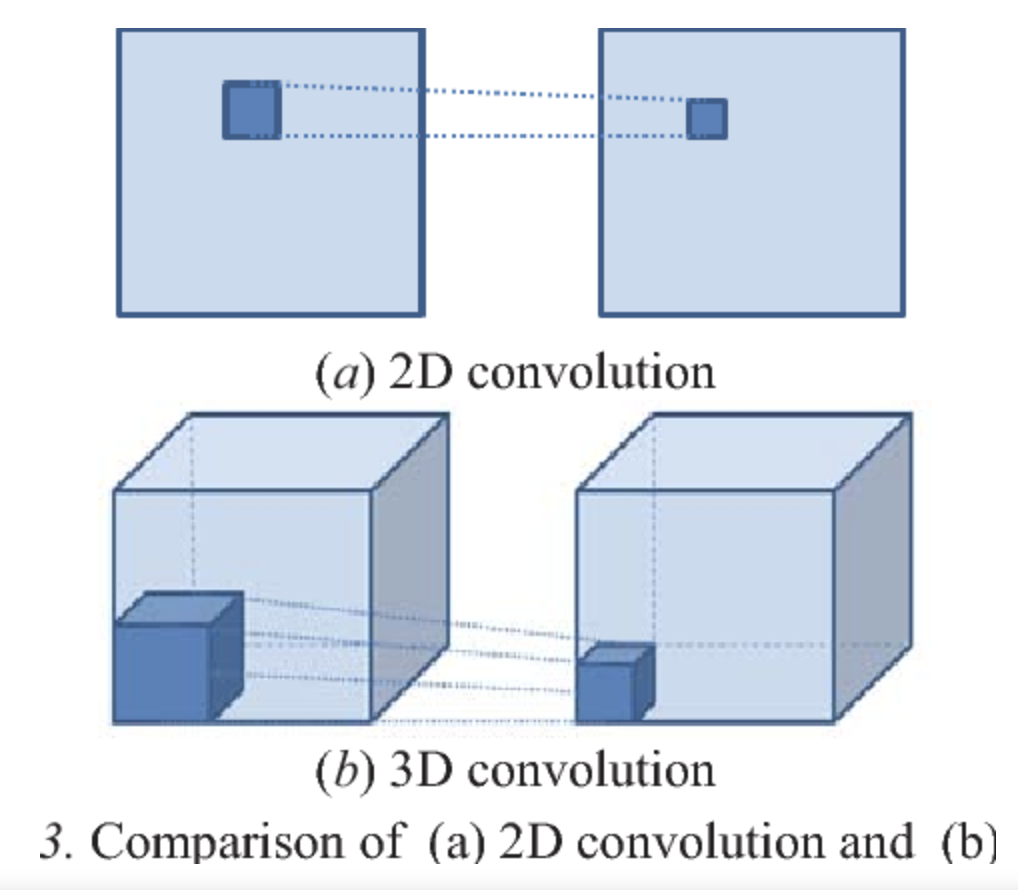
i couldn't exactly find an animation to show this for 3d convolutions, which are the same but with another dimension tacked on for analyzing volumes, but the idea is very similar: imagine a cool looking cube sliding through a volume, doing the same operations that we saw in the 2d case.
when we train such a network, we're basically optimizing the values in the kernel; we're making sure that the numbers we're multiplying by our 3d points will give us the highest classification accuracy, meaning we guess correctly what object belongs to which class.
this was just an explanation of the convolutional layers of the network; there is in fact much more going on underneath the hood, but better and more experienced authors than me have written about these in depth, and i encourage you to look at this article if you are interested. for now, i will borrow one of their images for my own benefit.
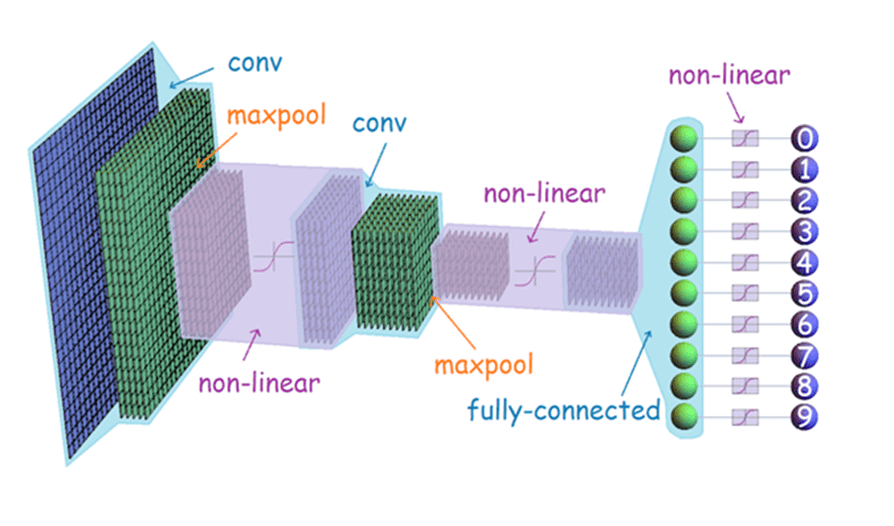
this approach actually worked! granted, we had to voxelize the point clouds so they'd place nice dimensionally (dimensionality and importing libraries, the two maladies that plague pytorch users relentlessly), but we got the training loop to run! this was not the first, second, third, or even fourth approach that we tried. i've already spoken about some of the experiments i tried, but my group mate spent a day trying to get a transfer learning approach to work; the idea was to take a pretrained model and tweak it a bit so it can learn the behavior of our data. this should have worked, but we were tragically hit with technical issue after technical issue, and, in the interest of time, and our own sanity, we had to create our own model.
the attentive reader will notice that many paragraphs ago, i said "problems", plural, and "first task", implying that there were more. task two had to do with semantic segmentation,
semantic segmentation is the process of classifying each pixel (or voxel, in 3d data) in an image or 3d scene into a category or "class." unlike object detection, which just draws boxes around objects, semantic segmentation gives a much richer understanding by labeling each individual part of the scene.
for example, imagine you have an image of a street scene. a semantic segmentation model would label each pixel as part of a "car," "road," "pedestrian," "building," "tree," etc. in a 3d point cloud, semantic segmentation would label each point as part of a specific object or surface — so every point on a car would be labeled "car," while every point on a sidewalk would be labeled "sidewalk."
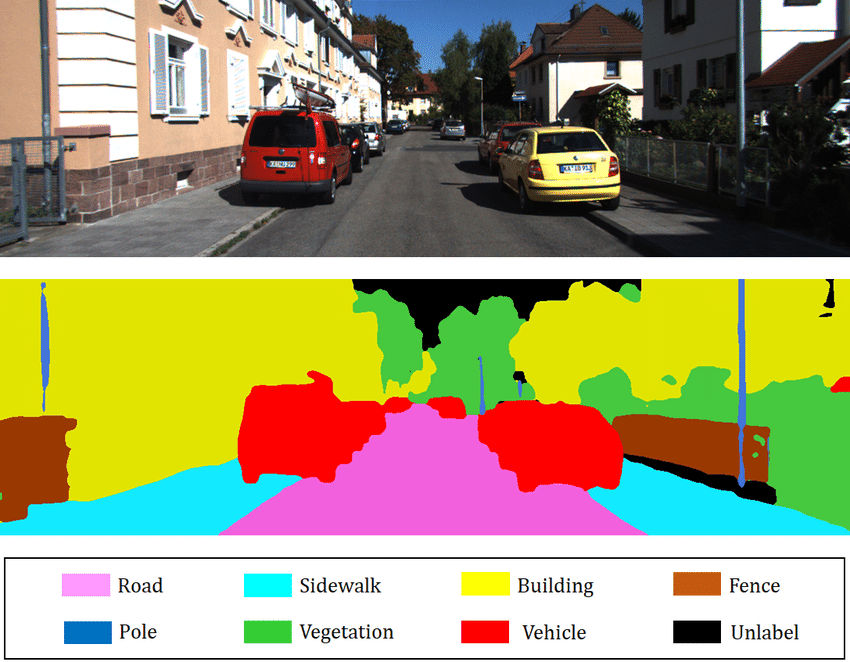
in short, if memory serves correct (i've been lazy, this event happened a month ago as of the time of me writing this article), none of the groups managed to get this to work, so we were all judged based on how well we could perform object detection.
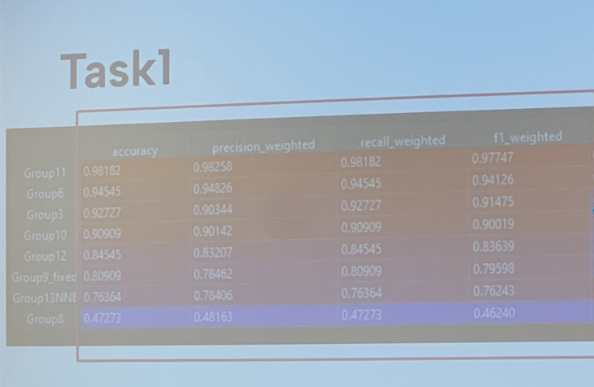
results
excuse the bad image quality, i think i was eating a piece of fruit with one hand while taking this photo from the crowd, but our little humble group of two people is group 10, and we had a 90.9% test accuracy when categorizing the different objects! (our validation accuracy was even better at 97%, but test accuracy is what counts). this means we got fourth place!
i'm very very happy about this result, but at the time, i was also completely mystified by how group 11 got 98.1% test set accuracy; this is nearly perfect. how was this achieved? what insane model could they be running? did they train it on a supercomputer? have they built the singularity? has agi arrived?
there is a paper written by hungarian-american physicist eugene wigner, titled "the unreasonable effectiveness of mathematics in the natural sciences". the very first paragraph of this paper relates the story of two old high school classmates reuniting and talking about their jobs. one is a statistician and shows the other his work on population trends, and explained to his old friend that you could learn information about population averages using something called the gaussian distribution. the classmate was doubtful, and asked, how can you know about population averages using that? the statistician indulged him, and showed him the formula for the gaussian distribution. "what is this symbol here?" asks the statisticians friend. "this is pi, the ratio of the circumference of any circle to its diameter" replies the statistician. "well, now you are pushing your joke too far," replies the statisticians friend, "surely the population has nothing to do with the circumference of the circle."
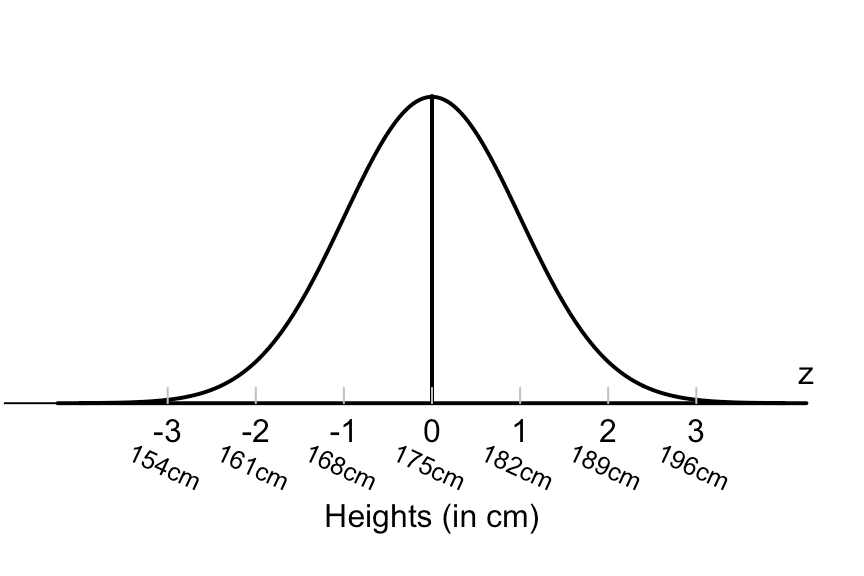
my point is; the paper is about how the math is so effective at modelling our world that it can sometimes contradict common sense. if i had to write a similar paper, it would be titled "the unreasonable effectiveness of random forests at doing literally any machine learning task". the number one group achieved a 98.1% test score accuracy with a random forest.
granted, i don't have a lot of experience to boast, so take this with many grains of salt, but in the research papers that i've read (mostly in quantitative chemistry!), and almost every single problem i've ever encountered, it was random forests (or a variant of them, such as boosted forests) that solved the problem most effectively, and simply. they are so good and so effective and so simple that i sometimes think somebody is pulling my leg. i have a hard time believing it sometimes. training and fitting a random forest using something like scikit-learn can be as simple as 5 lines of code.
this is where the foreshadowing from earlier is relevant. they trained on how big each object was. this was enough to tell them what the object was 98.1% of the time. this was the approach that i had in mind when doing my multilayer perceptron experiment. if i could get the code to work, i have no reason to believe it wouldn't achieve the exact same accuracy.
there is a lesson to be learned here. try all the "dumb" approaches before taking out the big guns. you might just hack your way to a 10.000 dkk first place prize with a simple solution, and baffle an entire audience of hackathon participants, along with the judges.
nevertheless, i'm obviously very happy about our performance. 4th place is very cool, especially considering our group was two people, and that i have never tried anything like this before. much thanks to the people of nne and clearedge3d for hosting, and thank you to my only group mate, who stuck with me through it all.
perhaps the next article on this page (hopefully uploaded before 2026), can be on random forests, and how we can use them to make lots of money.